Carthew Lab: Research
A Physical View of Cell Biology
The cells in our bodies must fit together seamlessly in tissues and organs, adopting specific shapes to function properly. How do cells change their order and shape to collectively form the complex organs of our bodies? What are the rules that carry this out, and can we harness these rules for tissue engineering and regenerative medicine? Cell biology has provided remarkable understanding about the molecules that regulate the coordinated change in cell shapes - morphogenesis. However, at times the molecules seem to confound rather than clarify. Why? In 1917, the English biologist D'Arcy Thompson proposed that morphogenesis should be thought of as a problem of mechanics, the branch of physics concerned with forces and motion. This highly original concept fell out of favor as the notion of genetic control of morphogenesis emerged. However, studies this past decade have revived the contention that mechanical forces are fundamental shapers of cells and tissues. They further suggest that, if used in a combinatorial manner, a small number of force-generating properties—namely cell-cell adhesion, cell-matrix adhesion, protrusion, and contractility—could orchestrate morphogenesis. An exciting new challenge in biophysics is to interpret the functions of molecules, as defined by cell biology, within the framework of the elementary forces that shape cells and tissues. This will provide the opportunity to unite a mechanical view of morphogenesis with modern molecular genetics, and to explain the bewildering variety of cell shapes, arrangements, and movements that are seen in life.
Blowing Bubbles
Thompson was fascinated by cells' tendencies to aggregate in ways that seemed to minimize their overall surface area. He drew analogy from a non-living model of mechanics studied by the physicist Joseph Plateau. Plateau described how soap bubbles are organized by surface minimization, and he observed that in stable aggregates, bubbles intersect at three-way vertices, the angle of which is regular and 120°. As Thompson noted, such geometric features are also observed in tissue epithelia where cells tend to form a hexagonal array. A hexagonal array of soap bubbles represents an energy minimum in which forces are balanced. Several years ago, we discovered a much more striking example of this phenomenon in the Drosophila eye (Hayashi and Carthew, 2004). The eye epithelium is composed of 800 repeating units of a small number of cells. Within each unit, two primary pigment cells surround four central cone cells and are in turn framed by secondary and tertiary pigment cells in a highly reproducible pattern. Our group genetically varied the number of cone cells in each unit, and we found that they packed into reproducible configurations that precisely resembled those of free soap bubble aggregates of the same number. In other words, cone cells changed shape so that the entire cluster reached an energetically favorable state, as also occurs with soap bubbles.
Cell membranes are not soap films and so a more realistic depiction of surface energy is needed. Thompson developed a simple theory based on interfacial tension to explain how cells arrange in tissues. Interfacial tension measures the energy required to increase the surface of contact between fluid-like entities like cells and bubbles. For cells, this tension is a function of simple surface tension as well as biological components such as cell-cell adhesion, which reduces interfacial tension. Adhesion is not the only biological component of cellular interfacial tension. The actin cytoskeleton and myosin motors responsible for inter-filament contraction contribute positively to interfacial tension.
Biophysical Modeling Coupled to Genetic Experimentation
In order to unite Thompson’s vision with modern biology, we have developed an interdisciplinary research team, combining the biological expertise of our group with expertise in the physics and theoretical mechanics of soft materials from Sascha Hilgenfeldt’s group at University of Illinois, Urbana Champaign. We think the time is right for coupling mechanics model-building with sophisticated molecular genetic experimentation, focused on tractable epithelial models. We have developed a cell-based physical model for interfacial tension that is both mathematical and based on the Drosophila eye. Beginning with virtual cells of random shape, a computer simulation allows the cells to change shape so as to achieve a minimal interfacial tension for the entire eye unit. The modeling quantitatively recapitulates the precise cell shapes found in the Drosophila eye (Hilgenfeldt et al., 2008). This mathematical approach to modeling cell shapes in epithelia is one of just a few being developed in the world.
It is well known that cell-cell adhesion can play an important role in morphogenesis of tissues. Cells in the Drosophila eye express two kinds of cell-cell adhesion molecules: E-cadherin and N-cadherin. All cells contain E-cadherin; however, only the four cone cells contain N-cadherin. The cadherin protein molecules become localized in a thin band of lateral cell membrane corresponding to the adherens junction, which is the major site of adhesion between cells. Cadherins in one membrane bind to cadherins located in the membrane of a neighboring cell across the intercellular gap, increasing the adherence of one cell with its neighbor. Adhesion between facing membranes decreases interfacial tension making expansion of the cell-cell interface energetically favorable. However, the expansion of one interface affects other cell-cell interfaces due to constraints on the overall size of the cell membrane. Shape changes in one cell induce shape changes in others, and alteration of the elastic energy of the membranes around all cells. Ultimately, the mechanical energy of the entire unit needs to be minimized globally in order to find an equilibrium configuration for the unit of cells.
We have used experimental genetics and computer modeling to understand how cadherin molecules control morphogenesis (Gemp et al., 2011). Comparison of model simulations with experimental data for mutants in which certain cells produce altered levels of cadherin have found that (i) the model describes characteristic shape changes in such mutants, (ii) the simulations distinguish between different mechanisms of how cadherin levels are attained and controlled, and (iii) the model incorporates important dynamical features in morphogenesis, such as the temporal sequence of cadherin expression and cell-cell contact remodeling.
The Future
Our objective is the biomechanical modeling of morphogenesis to enhance regenerative medicine and tissue engineering, where damaged tissue is therapeutically replaced. The research aims of this work are to experimentally measure and theoretically describe (i) the shape of a complete three-dimensional epithelium, (ii) characteristic changes in this shape during morphogenesis (attempting, for the first time, a rigorous description of the mechanics and mechanisms of elementary morphogenetic processes), and (iii) the regulation of the mechanical forces through the action of signal transduction pathways.
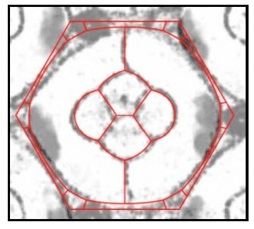
An overlay of two images. One image is a photomicrograph of a single eye unit with cell membranes visible in grey/black. The other image is a virtual eye unit from a computer simulation in which the unit’s total interfacial tension is minimized - virtual cell membranes appear red. The two images almost perfectly match.

Images on the left show eye units where there are five or six cone cells instead of four. Five cells always form one kind of configuration while six cells form one of three kinds of configurations. Middle images show stable aggregates of soap bubbles. Five bubbles always form one kind of configuration while six bubbles form one of three kinds of configurations. Remarkably, the number and quality of bubble configurations precisely match the cell configurations. This is true for bubble/cell numbers from one to four as well. Images on the right show virtual cells from computer simulations in which each unit’s total interfacial tension is minimized. These faithfully simulate the observed configurations.



The geometry of the Drosophila eye. (A) Cross section cartoon of one eye unit, with the “core” of cone and primary pigment cells and the “frame” of secondary and tertiary cells. (B) Side view of one unit with photoreceptor cells (R) below the adherens junction (AJ), and the lens (L) above it. (C) Double-stained confocal fluorescence image of the Drosophila eye. Staining highlights E-cadherin (green) and N-cadherin (red); where the two proteins are co-localized the color appears orange.
Northwestern University | Northwestern Search
Center for Cell and Developmental Systems Biology | Department of Molecular Biosciences
2205 Tech Drive, Hogan 2-100, Evanston, IL 60208 Email the Webmaster
WWW Disclaimer and University Policy Statements © 2011 Northwestern University